How Do You Know When to Use the Addition Property

Solving Linear Equations and Inequalities

17 Solve Equations Using the Subtraction and Addition Properties of Equality

Learning Objectives

By the cease of this section, you will be able to:

Verify a solution of an equation
Solve equations using the Subtraction and Add-on Properties of Equality
Solve equations that require simplification
Interpret to an equation and solve
Translate and solve applications

Verify a Solution of an Equation

Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to discover the value or values of the variable that make each side of the equation the same – and then that we end upwardly with a truthful statement. Any value of the variable that makes the equation true is called a solution to the equation. Information technology is the answer to the puzzle!

Solution of an equation

A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.

To determine whether a number is a solution to an equation.

Substitute the number in for the variable in the equation.
Simplify the expressions on both sides of the equation.
Decide whether the resulting equation is truthful (the left side is equal to the right side)
- If it is true, the number is a solution.
- If information technology is not true, the number is not a solution.

Determine whether $x=\frac{3}{2}$ is a solution of $4x-2=2x+1$ .

Is $y=\frac{4}{3}$ a solution of $9y+2=6y+3$ ?

Is $y=\frac{7}{5}$ a solution of $5y+3=10y-4$ ?

yeah

Solve Equations Using the Subtraction and Addition Properties of Equality

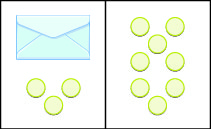
We are going to utilize a model to clarify the process of solving an equation. An envelope represents the variable – since its contents are unknown – and each counter represents one. We will set out one envelope and some counters on our workspace, as shown in (Figure). Both sides of the workspace have the aforementioned number of counters, merely some counters are "hidden" in the envelope. Can you tell how many counters are in the envelope?

The analogy shows a model of an equation with ane variable. On the left side of the workspace is an unknown (envelope) and 3 counters, while on the right side of the workspace are viii counters.

This image illustrates a workspace divided into two sides. The content of the left side is equal to the content of the right side. On the left side, there are three circular counters and an envelope containing an unknown number of counters. On the right side are eight counters.

What are you lot thinking? What steps are you taking in your heed to effigy out how many counters are in the envelope?

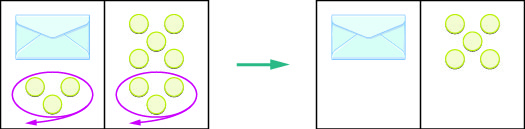
Perhaps you lot are thinking: "I demand to remove the three counters at the bottom left to become the envelope by itself. The 3 counters on the left tin exist matched with 3 on the correct and so I tin take them abroad from both sides. That leaves v on the correct—so there must be v counters in the envelope." See (Figure) for an illustration of this process.

The analogy shows a model for solving an equation with one variable. On both sides of the workspace remove three counters, leaving just the unknown (envelope) and 5 counters on the right side. The unknown is equal to 5 counters.

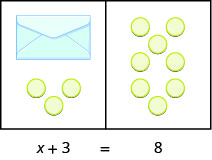
What algebraic equation would match this situation? In (Figure) each side of the workspace represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope $x$ .

The illustration shows a model for the equation $x+3=8$ .

Let's write algebraically the steps we took to notice how many counters were in the envelope:


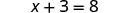Beginning, we took away three from each side.
Then nosotros were left with five.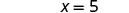

Check:

5 in the envelope plus three more does equal viii!

$5+3=8$

Our model has given u.s. an idea of what we need to do to solve ane kind of equation. The goal is to isolate the variable by itself on one side of the equation. To solve equations such every bit these mathematically, we apply the Subtraction Property of Equality.

Subtraction Holding of Equality

For any numbers a, b, and c,

$\begin{array}{ccccc}\text{If}\hfill & & \hfill a& =\hfill & b,\hfill \\ \text{then}\hfill & & \hfill a-c& =\hfill & b-c\hfill \end{array}$

When you subtract the aforementioned quantity from both sides of an equation, you still accept equality.

Doing the Manipulative Mathematics activity "Subtraction Property of Equality" volition help you develop a improve understanding of how to solve equations past using the Subtraction Property of Equality.

Permit'south see how to use this belongings to solve an equation. Think, the goal is to isolate the variable on i side of the equation. And we bank check our solutions past substituting the value into the equation to make certain we accept a true statement.

Solve: $y+37=-13.$

Solve: $x+19=-27$ .

$x=-46$

Solve: $x+16=-34$ .

$x=-50$

What happens when an equation has a number subtracted from the variable, as in the equation $x-5=8$ ? We employ another property of equations to solve equations where a number is subtracted from the variable. We want to isolate the variable, and then to 'undo' the subtraction we volition add the number to both sides. We use the Addition Property of Equality.

Addition Property of Equality

For whatever numbers a, b, and c,

$\begin{array}{ccccc}\text{If}\hfill & & \hfill a& =\hfill & b,\hfill \\ \text{then}\hfill & & \hfill a+c& =\hfill & b+c\hfill \end{array}$

When you add together the same quantity to both sides of an equation, you lot notwithstanding have equality.

In (Figure), 37 was added to the y and so we subtracted 37 to 'undo' the addition. In (Effigy), we volition demand to 'disengage' subtraction by using the Addition Property of Equality.

Solve: $a-28=-37.$

Solve: $n-61=-75.$

$n=-14$

Solve: $p-41=-73.$

$p=-32$

Solve: $x-\frac{5}{8}=\frac{3}{4}.$

Solve: $p-\frac{2}{3}=\frac{5}{6}.$

$p=\frac{9}{6}\phantom{\rule{0.2em}{0ex}}p=\frac{3}{2}$

Solve: $q-\frac{1}{2}=\frac{5}{6}.$

$q=\frac{4}{3}$

The next example will exist an equation with decimals.

Solve: $n-0.63=-4.2.$

Solve: $b-0.47=-2.1.$

$b=-1.63$

Solve: $c-0.93=-4.6.$

$c=-3.67$

Solve Equations That Crave Simplification

In the previous examples, we were able to isolate the variable with just one operation. About of the equations we encounter in algebra volition take more than steps to solve. Normally, we will need to simplify one or both sides of an equation before using the Subtraction or Add-on Properties of Equality.

You should ever simplify as much as possible before you try to isolate the variable. Remember that to simplify an expression means to do all the operations in the expression. Simplify one side of the equation at a fourth dimension. Note that simplification is dissimilar from the process used to solve an equation in which we apply an operation to both sides.

How to Solve Equations That Crave Simplification

Solve: $9x-5-8x-6=7.$

Solve: $8y-4-7y-7=4.$

$y=15$

Solve: $6z+5-5z-4=3.$

$z=2$

Solve: $5\left(n-4\right)-4n=-8.$

Solve: $5\left(p-3\right)-4p=-10.$

$p=5$

Solve: $4\left(q+2\right)-3q=-8.$

$q=-16$

Solve: $3\left(2y-1\right)-5y=2\left(y+1\right)-2\left(y+3\right).$

Solve: $4\left(2h-3\right)-7h=6\left(h-2\right)-6\left(h-1\right).$

$h=6$

Solve: $2\left(5x+2\right)-9x=3\left(x-2\right)-3\left(x-4\right).$

$x=2$

Translate to an Equation and Solve

To solve applications algebraically, we will begin by translating from English language sentences into equations. Our starting time footstep is to look for the discussion (or words) that would interpret to the equals sign. (Effigy) shows us some of the words that are commonly used.

Equals =
is is equal to is the same every bit the effect is gives was volition be

The steps nosotros use to interpret a sentence into an equation are listed beneath.

Translate an English sentence to an algebraic equation.

Locate the "equals" word(s). Translate to an equals sign (=).
Translate the words to the left of the "equals" discussion(s) into an algebraic expression.
Interpret the words to the right of the "equals" word(s) into an algebraic expression.

Translate and solve: Eleven more than x is equal to 54.

Translate and solve: 10 more than x is equal to 41.

$x+10=41;x=31$

Interpret and solve: Twelve less than ten is equal to 51.

$y-12=51;y=63$

Translate and solve: The deviation of $4x$ and $3x$ is 14.

$4x-3x=14;x=14$

Translate and solve: The deviation of $7a$ and $6a$ is $-8$ .

$7a-6a=-8;a=-8$

Translate and Solve Applications

Most of the fourth dimension a question that requires an algebraic solution comes out of a real life question. To begin with that question is asked in English (or the language of the person asking) and not in math symbols. Because of this, information technology is an important skill to exist able to translate an everyday situation into algebraic language.

Nosotros will start by restating the problem in just one judgement, assign a variable, and and so interpret the sentence into an equation to solve. When assigning a variable, choose a letter that reminds you of what yous are looking for. For case, you lot might utilize q for the number of quarters if you were solving a problem about coins.

How to Solve Translate and Solve Applications

The MacIntyre family recycled newspapers for two months. The 2 months of newspapers weighed a total of 57 pounds. The second month, the newspapers weighed 28 pounds. How much did the newspapers weigh the kickoff calendar month?

Translate into an algebraic equation and solve:

The Pappas family has two cats, Zeus and Athena. Together, they weigh 23 pounds. Zeus weighs xvi pounds. How much does Athena weigh?

seven pounds

Translate into an algebraic equation and solve:

Sam and Henry are roommates. Together, they accept 68 books. Sam has 26 books. How many books does Henry have?

42 books

Solve an application.

Read the problem. Brand certain all the words and ideas are understood.
Place what we are looking for.
Proper noun what we are looking for. Choose a variable to correspond that quantity.
Translate into an equation. It may exist helpful to recapitulate the problem in one sentence with the of import data.
Solve the equation using good algebra techniques.
Check the reply in the problem and brand sure information technology makes sense.
Answer the question with a complete judgement.

Randell paid ?28,675 for his new car. This was ?875 less than the sticker cost. What was the sticker price of the automobile?

Translate into an algebraic equation and solve:

Eddie paid ?19,875 for his new car. This was ?1,025 less than the sticker price. What was the sticker cost of the car?

?twenty,900

Interpret into an algebraic equation and solve:

The access price for the movies during the day is ?7.75. This is ?3.25 less the price at night. How much does the movie cost at night?

?11.00

Cardinal Concepts

To Determine Whether a Number is a Solution to an Equation
1. Substitute the number in for the variable in the equation.
2. Simplify the expressions on both sides of the equation.
3. Determine whether the resulting statement is true.
  - If it is true, the number is a solution.
  - If it is not true, the number is not a solution.
Improver Property of Equality
Subtraction Property of Equality
To Translate a Sentence to an Equation
1. Locate the "equals" word(s). Interpret to an equal sign (=).
2. Translate the words to the left of the "equals" word(s) into an algebraic expression.
3. Translate the words to the correct of the "equals" word(s) into an algebraic expression.
To Solve an Application
1. Read the problem. Make certain all the words and ideas are understood.
2. Identify what nosotros are looking for.
3. Proper name what nosotros are looking for. Choose a variable to correspond that quantity.
4. Translate into an equation. Information technology may be helpful to restate the trouble in i sentence with the important information.
5. Solve the equation using good algebra techniques.
6. Check the respond in the problem and make sure it makes sense.
7. Reply the question with a complete sentence.

Do Makes Perfect

Verify a Solution of an Equation

In the post-obit exercises, determine whether the given value is a solution to the equation.

Is $y=\frac{5}{3}$ a solution of
$6y+10=12y$ ?

yep

Is $x=\frac{9}{4}$ a solution of
$4x+9=8x$ ?

Is $u=-\frac{1}{2}$ a solution of
$8u-1=6u$ ?

Is $v=-\frac{1}{3}$ a solution of
$9v-2=3v$ ?

Solve Equations using the Subtraction and Add-on Properties of Equality

In the following exercises, solve each equation using the Subtraction and Improver Properties of Equality.

$x+24=35$

$x=11$

$x+17=22$

$y+45=-66$

$y=-111$

$y+39=-83$

$b+\frac{1}{4}=\frac{3}{4}$

$b=\frac{1}{2}$

$a+\frac{2}{5}=\frac{4}{5}$

$p+2.4=-9.3$

$p=-11.7$

$m+7.9=11.6$

$a-45=76$

$a=121$

$a-30=57$

$m-18=-200$

$m=-182$

$m-12=-12$

$x-\frac{1}{3}=2$

$x=\frac{7}{3}$

$x-\frac{1}{5}=4$

$y-3.8=10$

$y=13.8$

$y-7.2=5$

$x-165=-420$

$x=-255$

$z-101=-314$

$z+0.52=-8.5$

$z=-9.02$

$x+0.93=-4.1$

$q+\frac{3}{4}=\frac{1}{2}$

$q=-\frac{1}{4}$

$p+\frac{1}{3}=\frac{5}{6}$

$p-\frac{2}{5}=\frac{2}{3}$

$p=\frac{16}{15}$

$y-\frac{3}{4}=\frac{3}{5}$

Solve Equations that Require Simplification

In the following exercises, solve each equation.

$c+31-10=46$

$c=25$

$m+16-28=5$

$9x+5-8x+14=20$

$x=1$

$6x+8-5x+16=32$

$-6x-11+7x-5=-16$

$x=0$

$-8n-17+9n-4=-41$

$9\left(y-2\right)-8y=-16$

$8\left(u+1.5\right)-7u=4.9$

$u=-7.1$

$5\left(w+2.2\right)-4w=9.3$

$6a-5\left(a-2\right)+9=-11$

$a=-30$

$8c-7\left(c-3\right)+4=-16$

$y=28$

$n=-50$

$\text{−}\left(j+2\right)+2j-1=5$

$j=8$

$\text{−}\left(k+7\right)+2k+8=7$

$\text{−}\left(\frac{1}{4}a-\frac{3}{4}\right)+\frac{5}{4}a=-2$

$a=-\frac{11}{4}$

$\text{−}\left(\frac{2}{3}d-\frac{1}{3}\right)+\frac{5}{3}d=-4$

$x=13$

Interpret to an Equation and Solve

In the following exercises, translate to an equation and so solve information technology.

Nine more than than $x$ is equal to 52.

$x+9=52;x=43$

The sum of ten and $-15$ is 23.

10 less than m is $-14$ .

$m-10=-14;m=-4$

Three less than y is $-19$ .

The sum of y and $-30$ is 40.

$y+\left(-30\right)=40;y=70$

Twelve more than p is equal to 67.

The deviation of $9x\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}8x$ is 107.

$9x-8x=107;107$

The difference of $5c\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}4c$ is 602.

The departure of $n$ and $\frac{1}{6}$ is $\frac{1}{2}$ .

$n-\frac{1}{6}=\frac{1}{2};\frac{2}{3}$

Translate and Solve Applications

In the following exercises, translate into an equation and solve.

Distance Avril rode her bike a total of 18 miles, from home to the library and then to the beach. The altitude from Avril'due south house to the library is vii miles. What is the distance from the library to the beach?

xi miles

Reading Jeff read a total of 54 pages in his History and Folklore textbooks. He read 41 pages in his History textbook. How many pages did he read in his Folklore textbook?

Age Eva's daughter is 15 years younger than her son. Eva'due south son is 22 years old. How old is her daughter?

7 years old

Age Pablo's father is iii years older than his mother. Pablo'due south female parent is 42 years erstwhile. How old is his male parent?

Groceries For a family birthday dinner, Celeste bought a turkey that weighed v pounds less than the one she bought for Thanksgiving. The birthday turkey weighed xvi pounds. How much did the Thanksgiving turkey weigh?

21 pounds

Weight Allie weighs 8 pounds less than her twin sister Lorrie. Allie weighs 124 pounds. How much does Lorrie weigh?

Health Connor's temperature was 0.seven degrees higher this forenoon than it had been last nighttime. His temperature this morn was 101.2 degrees. What was his temperature last night?

100.v degrees

Health The nurse reported that Tricia's daughter had gained 4.ii pounds since her terminal checkup and at present weighs 31.half-dozen pounds. How much did Tricia's daughter counterbalance at her concluding checkup?

Bacon Ron's paycheck this week was ?17.43 less than his paycheck final calendar week. His paycheck this calendar week was ?103.76. How much was Ron'southward paycheck final calendar week?

?121.19

Textbooks Melissa's math book toll ?22.85 less than her art volume cost. Her math book cost ?93.75. How much did her fine art book price?

Everyday Math

Writing Exercises

Is $-8$ a solution to the equation $3x=16-5x$ ? How exercise you know?

No. Justifications will vary.

What is the showtime footstep in your solution to the equation $10x+2=4x+26$ ?

Self Check

ⓐ Subsequently completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

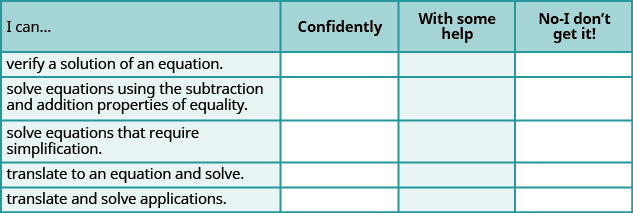
This is a table that has six rows and four columns. In the first row, which is a header row, the cells read from left to right

ⓑ If most of your checks were:

…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills yous used so that you tin continue to use them. What did you practise to become confident of your power to practice these things? Be specific!

…with some assist. This must be addressed quickly as topics you exercise not master become potholes in your road to success. Math is sequential – every topic builds upon previous piece of work. It is important to make sure you have a strong foundation before yous move on. Who can you lot ask for aid? Your swain classmates and instructor are expert resources. Is there a place on campus where math tutors are available? Can your study skills exist improved?

…no – I don't go it! This is critical and you must non ignore it. You demand to become help immediately or you will quickly exist overwhelmed. See your teacher every bit soon equally possible to discuss your state of affairs. Together you can come up up with a program to go you the assist you need.

Glossary

solution of an equation: A solution of an equation is a value of a variable that makes a truthful statement when substituted into the equation.

nelsonstentartudge.blogspot.com

Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/solve-equations-using-the-subtraction-and-addition-properties-of-equality/

How Do You Know When to Use the Addition Property

17 Solve Equations Using the Subtraction and Addition Properties of Equality

Learning Objectives

Verify a Solution of an Equation

Solve Equations Using the Subtraction and Addition Properties of Equality

Solve Equations That Crave Simplification

Translate to an Equation and Solve

Translate and Solve Applications

Cardinal Concepts

Do Makes Perfect

Everyday Math

Writing Exercises

Self Check

Glossary

0 Response to "How Do You Know When to Use the Addition Property"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel